There is a disagreement between pollsters about how well the Labour party is doing. Among the established and respected major pollsters, there are two camps. One group thinks that Labour is doing relatively well and will get more votes than any other party. But the other thinks Labour is doing less well and is in third or fourth place.
Curiously, the first group consists of all but one of the major pollsters, while the second consists of YouGov alone.
We can see the difference by looking at recent polls from both YouGov and non-YouGov pollsters. A poll-of-polls of four recent polls from non-YouGov pollsters (ComRes, Survation, Opinium, Ipsos-MORI) is shown on the left, along with the Electoral Calculus seat prediction. On the right is a poll-of-polls for four recent YouGov polls.
Labour/Lib Dem Coalition
|
| Party | Non-YouGov polls | Predicted Seats |
|---|---|---|
| CON | 24.3% | 220 |
| LAB | 26.5% | 281 |
| LIB | 18.3% | 57 |
| Brexit | 18.3% | 20 |
| Green | 6.0% | 1 |
| SNP | 3.2% | 50 |
Prediction based on 4 non-YouGov opinion
polls from 21 Jun 2019 to 16 Jul 2019,
sampling 6,095 people.
| Party | YouGov polls | Predicted Seats |
|---|---|---|
| CON | 23.8% | 213 |
| LAB | 19.8% | 182 |
| LIB | 19.5% | 68 |
| Brexit | 21.3% | 116 |
| Green | 9.0% | 1 |
| SNP | 3.2% | 50 |
Prediction based on 4 YouGov opinion polls
from 24 Jun 2019 to 17 Jul 2019,
sampling 7,084 people.
In the first scenario, Labour is on 26pc support and has enough seats to form a minority government with the Liberal Democrats. Together those two parties would have a majority of 48 seats in the House of Commons and Jeremy Corbyn would be Prime Minister.
But in the second scenario, Labour is only on 20pc and loses around a hundred seats. In this case, the Conservatives and Brexit party would have a slender Commons' majority of 8 seats and Boris Johnson would be Prime Minister.
Those two outcomes are obviously quite different.
How should we assess which outcome is more likely? Which pollster is more likely to be accurate? If we had no other information, it would be tempting to regard YouGov as a deviant pollster and ignore it. But we have some relevant information from the recent European elections. There was a similar divergence between the pollsters at that time.
The table below shows the average polls for the European elections in Britain, broken down between the non-YouGov pollsters and YouGov itself.
| Party | Non-YouGov Estimate | YouGov Estimate | Actual Result |
|---|---|---|---|
| CON | 12% | 8% | 9% |
| LAB | 23% | 14% | 14% |
| LIB | 14% | 17% | 20% |
| Brexit | 31% | 35% | 32% |
| Green | 7% | 11% | 12% |
| Ave Error | 4.5% | 1.7% | — |
Non-YouGov polls based on 16 non-YouGov polls taken between 1-22 May 2019, with a total sample size of 33,000 from BMG, Kantar, Panelbase, Opinium, Survation, ComRes, Hanbury Strategy. YouGov polls based on four YouGov polls taken between 8-21 May 2019, with a total sample size of 22,000. Polls were weighted to give more weight to later polls and to the latest poll from each pollster.
It is notable that YouGov also predicted that Labour would do worse than the other pollsters were predicting, and that YouGov was correct. YouGov showed an average Labour support of 14pc, which was correct to the nearest percentage point. They also had more accurate predictions for the Conservatives, Liberal Democrats and the Greens. Their only exception was the Brexit party which they overestimated by 3pc. The size of the average YouGov error across all five major parties was 1.7pc, which was much smaller than the average error for the other pollsters.
This evidence makes it hard to dismiss the YouGov results as an obvious error. They have been right before.
Although the YouGov polls are a little bit different from the others, how can it translate into such a large difference in seats? Is this real, or is there a problem with the model?
Firstly, the difference in Labour support is not that small. YouGov are measuring Labour's support at 7pc lower than the other pollsters. That is quite a large gap in electoral terms, and is also well outside the random sampling error for a reasonably-sized poll. But the question remains: would Labour really lose 110 seats if they lost "just" 7pc national support?
We can answer this question by looking at sensitivity analysis. This means altering the predicted vote share for any party by a small amount and seeing how many seats are predicted to change hands.
In this experiment we take the current Electoral Calculus headline prediction and perturb the Labour vote share up or down by up to 3pc (scaling the other parties multiplicatively to maintain the total vote) and re-calculate the number of seats won.
| Shock | Predicted LAB Seats | Change in LAB seats |
|---|---|---|
| -3% | 212 | -43 |
| -2% | 227 | -28 |
| -1% | 242 | -13 |
| 0% | 255 | 0 |
| +1% | 271 | 16 |
| +2% | 283 | 28 |
| +3% | 300 | 45 |
Although it is not exact, we can see that each 1pc change in support is worth around 14 seats to Labour. An increase in support means a gain in seats, and a decrease of support means a loss in seats. Indeed we can fit the best straight line through these points. The graph shows the seven data points (red dots) plus the green line of best fit.
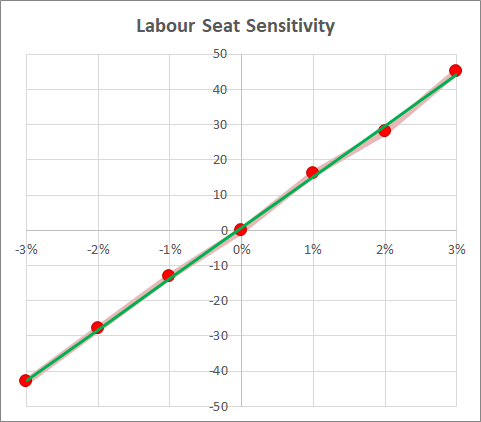
The fit is actually very good, and shows the slope of the best-fit line is 14. This means that Labour gains around 14 seats for every percent it gains in national support, and loses around 14 seats for every percent of national support which it loses.
This sensitivity factor is called the seat delta.
[Technical note: some readers with a technical background may be reminded of derivatives from differential calculus. The two concepts are indeed very similar. But since the number of seats won is integer-valued, differential calculus is less helpful because infinitesimal increments would mostly give a zero derivative. To get around that, we have to use larger increments such as 1pc.]
Although the seat delta will not work exactly for very large swings, it does give a sensible idea of the likely scale of change. YouGov see Labour with 6.8pc less support than the other pollsters, which should translate into a reduction in seats of around 6.8×14, which is ninety-five. And, give or take, that is close to the 99 seats which the model predicted Labour would lose under the YouGov polling.
We can calculate the seat deltas for the other parties in a similar way. The table below shows the results.
| Party | Predicted Votes | Predicted Seats | Seat Delta (Seats per 1pc) |
|---|---|---|---|
| CON | 23.2% | 196 | 27 |
| LAB | 25.0% | 255 | 14 |
| LIB | 17.9% | 60 | 6 |
| Brexit | 20.3% | 67 | 26 |
| Green | 6.8% | 1 | 0 |
The Conservative and Brexit parties have the largest seat deltas, with values around 25 seats per 1pc. This means that an increase of 1pc in national support could gain either of those parties about 25 seats and a decrease of 1pc could lose them about 25 seats. The Liberal Democrats have a smaller delta of only about 6 seats per 1pc change in vote share. The Greens have an almost zero delta at current support levels because it is hard for them to win seats as the smallest party in a five-party system.
It is useful to know that the seat deltas are not constant. Firstly, they vary with party support. Typically parties have the maximum delta when their support is between 20pc and 35pc, with the peak delta around 20pc-25pc for Conservative, Brexit and Green parties; while Labour and the Liberal Democrats have their peak delta when their support is around 30pc-35pc. Secondly, the seat deltas will be different under different models. Using the old UNS (uniform national swing) model, the seat deltas are much smaller than with the current regression-based model. Under other seat predictor models, the seat deltas are a little different but broadly similar.
Seat Deltas provide a good way of quickly estimating the confidence intervals of any prediction. The basic idea is to take the margin of error in the percentage support and multiply it by the seat delta to get the margin of error in the predicted seats.
For example, suppose an individual poll has a sample size of 2,000 people, and has a Labour vote share of 25pc. The margin of error due to random sampling error, with 95pc confidence, is 1.9pc. Using the Labour seat delta of 14 seats per 1pc, that would give a Labour seat error of 27 seats.
That error can be reduced by taking an average over several polls. Using a poll-of-polls with a total sample size of 10,000, the margin of error in the Labour vote share reduces to 0.85pc, and the seat uncertainty becomes just 12 seats. This means that we would be 95pc confident that the number of seats won by Labour would be between 243 and 267.
This calculation can be repeated for every major party, which gives the following 95pc confidence bounds.
| Party | Predicted Votes | Predicted Seats | Margin of error in vote share | Margin of error in seats | Low Seats | High Seats |
|---|---|---|---|---|---|---|
| CON | 23.2% | 196 | ±0.83% | 22 | 174 | 218 |
| LAB | 25.0% | 255 | ±0.85% | 12 | 243 | 267 |
| LIB | 17.9% | 60 | ±0.75% | 4 | 56 | 64 |
| Brexit | 20.3% | 67 | ±0.79% | 20 | 47 | 87 |
| Green | 6.8% | 1 | ±0.49% | 0 | 1 | 1 |
These bounds are quite tight. They show, for instance, that Labour and the Liberal Democrats (plus the SNP in some scenarios) could always form a government. And also that the Conservative and Brexit parties, even in their best scenarios, would not have a majority together.
But we also notice that the random sampling error is much smaller than the methodology difference between the pollsters. The next table shows the difference between the YouGov polling and the non-YouGov polling in terms of both vote share and predicted seats. The differences can be as high as 7pc in vote share and 155 in terms of seats, which is much larger than the random sampling error.
| Party | Methodology Vote difference | Methodology Seat difference |
|---|---|---|
| CON | -0.5% | −7 |
| LAB | -6.8% | −99 |
| LIB | 1.3% | 11 |
| Brexit | 3.0% | 96 |
| Green | 3.0% | 0 |
There is a significant difference between YouGov and the other pollsters. The difference could be worth a hundred seats to the major parties. This seat difference is well-explained by applying the concept of "seat deltas" to the difference in vote share between the pollsters. The seat deltas also provide a convenient way to estimate seat-based confidence intervals.
The difference between YouGov and the other pollsters is much larger than random sampling error, and indicates some methodological difference. The difference is similar to that shown at the recent European elections. In that case, YouGov were more accurate on average than the other pollsters.
This pollster difference adds to the uncertainty of the current four-party environment. And this difference should be watched carefully to see if it shrinks over time. But, if it doesn't, then we will have to decide where the truth lies.
Return to Articles home page.
©2019 Electoral Calculus